What is Big O Notaion ?

Big O Notation is a way to measure how well a computer algorithm scales as the number of data increases, so when you have to choose an approach to create your system Big O Notation will help you to select the most efficient solution,

The Big-O notation measures the worst-case complexity of an algorithm. In Big-O notation, n represents the number of inputs.

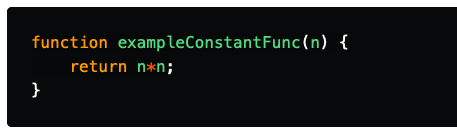
Constant time (O(1))

O(1) does not change with respect to input space. Hence, O(1) is referred to as being constant time.
An exmple of an of an O(1):

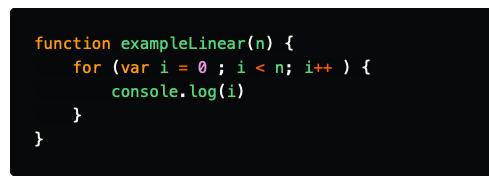
Linear time (O(n))

O(n) is linear time and applies to algorithms that must do n operations in the worst-case scenario. most its just A simple basic loop that within it we perform constant time operations.
An exmple of an of an O(n):

Logarithmic time O(log(n))

A Logarithmic time function is one in which the time of execution is proportional to the logarithm of the input size.
Consider the following example:

We can see that in any given iteration, the value of i = 2i, so in the nth iteration, the value of i= 2n. Also, we know that the value of i is always less than the size of the loop itself (N).
From that, we can deduce the following result:
2^n < N
log(2^n) < log(N)
n < log(N)
From the preceding code, we can see that the number of iterations would always be less than the log on the input size. Hence, the worst-case time complexity of such an algorithm would be O(log(n)). The efficiency of logarithmic time complexities is apparent with large inputs such as a million items.

Quadratic time(O(n^2 ))

With quadratic time algorithms, we have now entered the dark side of the time complexity.
As the name suggests, the size of the input quadratically affects the running time of the algorithm. One common example is nested loops:

As you can see from the preceding example, for i = 0, the inner loop runs n times, and the same for i = 1, and i = 2, and so on. The inner loop always runs n times and is not dependent on the value of n, thus making the algorithms time complexity O(n2).

Polynomial time(O(nn))

Polynomial-time complexity is the running time complexity of algorithms, which runs to the order of nk. Quadratic time algorithms are certain types of polynomial-time algorithms where k = 2. A very simple example of such an algorithm would be as follows:

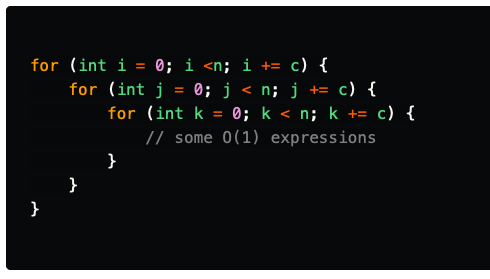As you can see, this example is just an extension of the example in the quadratic time section. The worst-case complexity of this case is O(n3). As you can see, this example is just an extension of the example in the quadratic time section. The worst-case complexity of this case is O(n3).

Rules of Big-O Notation

Let’s represent an algorithm’s complexity as f(n). n represents the number of inputs, f(n)time represents the time needed, and f(n)space represents the space (additional memory) needed for the algorithm. The goal of algorithm analysis is to understand the algorithm’s efficiency by calculating f(n). However, it can be challenging to calculate f(n). Big-O notation provides some fundamental rules that help developers compute for f(n).

Coefficient Rule: “Get Rid of Constants”

Let’s first review the coefficient rule. This rule is the easiest rule to understand. It simply requires you to ignore any non-input-size-related constants. Coefficients in Big-O are negligible with large input sizes. Therefore, this is the most important rule of Big-O notations.
If f(n) is O(g(n)), then kf(n) is O(g(n)), for any constant k > 0.
This means that both 5f(n) and f(n) have the same Big-O notation of O(f(n)). Here is an example of a code block with time complexity of O(n):
This block of code has f(n) = n. This is because it adds to count n times. Therefore, this function is O(n) in time complexity: